Machine learning large-angle convergent-beam electron diffraction

Session

Poster Session 3

Authors

Mr Jeremy Thorn (1), Mr James Partington (1), Prof Rudolf Roemer (1), Prof Richard Beanland (1)

Affiliations

1. University of Warwick

Keywords

Machine learning, simulation, electron diffraction, bloch waves

Abstract text

The theory of electron scattering by crystalline materials is well-established, with two main approaches to the calculation of diffracted intensities: the Bloch-wave (or scattering matrix) method, and the Multislice method [1, 2]. Both have been implemented in numerous simulation programs and compute the required large-angle convergent beam electron diffraction (LACBED) patterns. While the accuracy of these simulations can be very high [3] they are also computationally intensive and relatively slow even with modern high-performance computing facilities and graphical processing units (GPUs). In Bloch-wave simulations the limiting step is the inversion of a complex, non-Hermitian matrix, while for multislice the use of many configurations in the frozen-phonon approximation can increase simulation times by several orders of magnitude [1, 2]. As a result, simulation times are generally several minutes at best.

Machine learning (ML) as a computational approach has been gaining prominence in recent years and the implementation of neural networks as universal approximators holds great promise for the solution of inverse and/or computationally diffcult problems. Importantly, once trained, an ML calculation is fast - typically a few milliseconds on a GPU. In the case of modelling electron scattering, this may allow an increase in speed of 5-6 orders of magnitude.

Here, we explore the simulation of electron scattering using a variational autoencoder (VAE) [4]. The VAE takes as an input a 128x128 pixel image of the projected potential of a unit cell of cubic material in the [001] orientation and gives an output of the 000 LACBED pattern of the same size. The VAE is trained end-to-end using 5527 Felix [5] Bloch-wave simulations of cubic materials taken from the inorganic crystal structure database (ICSD).[6] The simulations were split 85:10:5 into training, validation, and test sets. Similarity was quantified using a zero-mean normalised cross correlation loss function Z.[7] The position of features in reciprocal space was fixed by choosing an angular range that varied in inverse proportion with lattice parameter. Typical patterns are shown in (Fig. 1a). Using 500 Bloch waves, each simulation typically required ~ 400 seconds to complete running on a cluster of 160 cores.

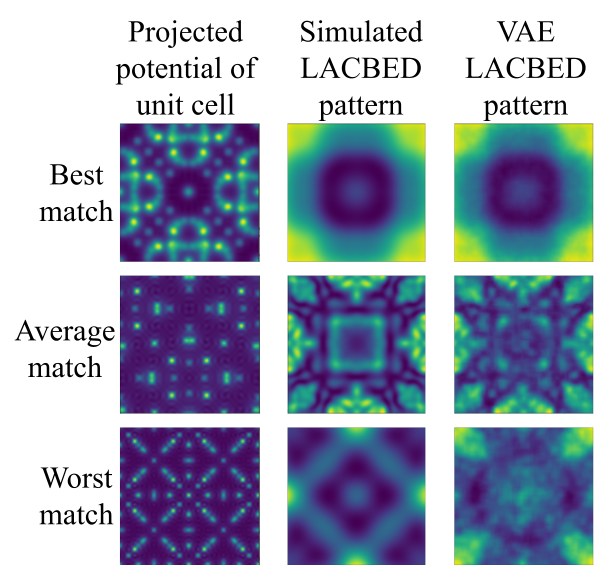
The VAE uses convolutional encoder and decoder sub-models, both 2 layers deep, to access a 12-dimensional latent space of encoded LACBED patterns. Calculations on an Nvidia GTX 1080Ti GPU are ~ 3:6 x 10⁵ times faster than a 160-core felix simulation. In this exploratory trial, only 5527 out of the 42879 cubic materials available on the ICSD were used for model training. Even with this limited training data set, some VAE simulations approach the accuracy of felix (top row, Fig. 1b), while others only produce a poor approximation (bottom row, Fig. 1b). We estimate that training on > 12000 simulations would produce losses Z < 5%, giving a similarity equivalent to that between felix and experiment.[8]

Figure 1: (a) Montage of Bloch-wave simulated 000 LACBED patterns
from twenty different cubic materials with incident beam orientation [001].
(b) Three examples of the VAE simulations with varying levels of similarity.
The best, average and worst match give Z = 0:22 %, 9:6 % and 130 %.

References

[1] B. G. Mendis, Electron beam-specimen interactions and simulation meth-
ods in microscopy (John Wiley, 2018).
[2] E. J. Kirkland, Advanced computing in electron microscopy (Springer, 1998).
[3] L. J. Allen et al., Ultramicroscopy 151, 11 (2015).
[4] D. P. Kingma and M. Welling, in Auto-encoding variational bayes (International
Conference on Learning Representations, ICLR, 2014).
[5] R. Beanland, K. Evans, R. A. Romer, and A. J. M. Hubert, Felix Bloch
wave simulation: https://github.com/RudoRoemer/Felix, 2021.
[6] A. Belsky, et al. Acta Cryst B 58,
364 (2002).
[7] R. Beanland et al. Acta Crystallographica Section A 77, (2021).
[8] A. J. M. Hubert, R. Romer, and R. Beanland, Ultramicroscopy 198, 1
(2019).