Understanding Trainable Segmentation for Inorganic Nanoparticle Images

Session

Stream 2: EMAG - Automated Control, Advanced Data Processing

Authors

Mr Cameron Bell (1, 5), Mr Kevin Treder (3), Dr Chen Huang (3, 4), Dr Manfred Schuster (2), Dr Judy Kim (3, 4), Prof Angus Kirkland (3, 4), Dr Thomas Slater (1)

Affiliations

1. Diamond Light Source
2. Johnson Matthey
3. University of Oxford
4. Rosalind Franklin Institute
5. University of Edinburgh

Keywords

image segmentation,

nanoparticles,

transmission electron microscopy

Abstract text

We have implemented a trainable segmentation interface in the ParticleSpy Python package, which is built on the widely-used HyperSpy package. We have investigated the use of different classifiers and filter kernels to determine optimal parameters for segmentation of metal nanoparticles from transmission electron microscope (TEM) and scanning transmission electron microscope (STEM) images. We compare our results to global segmentation and trained convolutional neural networks.

Imaging of inorganic nanoparticles in the TEM/STEM is a ubiquitous method of determining their size and shape in a straightforward way ^[1]. To accurately extract particle information, it’s necessary to segment particles from the image background. This is most widely performed using global intensity thresholds that can be manually determined, or can be calculated using a range of algorithms (e.g. Otsu’s method ^[2]). Global thresholding relies on a clear difference in intensities between particles and background, which is not always apparent.

Instead of segmenting based solely on image intensity, a number of methods have been developed that use a set of images that have been convolved with different filter kernels. Filter kernels convolve a small matrix with an image to isolate characteristics of the image, such as edges, textures, or intensity such as local minima or maxima. These filter kernels generate a set of features from the image which can then be used to train a classifier based on a set of user labelled pixels. The classifier ‘learns’ from the training data by defining boundaries between the background-labelled and particle-labelled pixels, determined from filter kernel values. The rest of the image or additional images can be classified using this trained classifier. This process is typically referred to as ‘trainable segmentation’ ^[3].

Our aim was to produce effective and versatile trainable segmentation capable of rapid segmentation from a small sample of user–labelled pixels, and to understand the effective classifiers and filter kernels used in ParticleSpy.

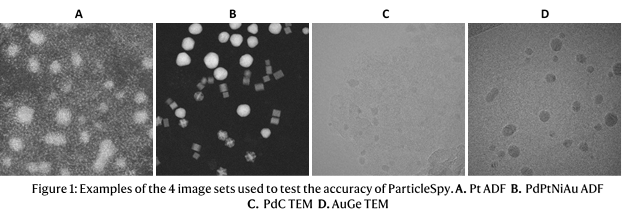
We tested our trainable segmentation algorithm on 4 sets of images in order to test the algorithm on images with different features and contrast: 2 HAADF­­–STEM image sets with Pt nanoparticles on one and a mixture of Pd, PtNi and Au nanoparticles on the other, and 2 TEM image sets with Pd nanoparticles and Au nanoparticles (displayed in Figure 1).

Figure 2 shows the Balanced Accuracy, for each image type segmented by both global thresholding and trainable segmentation. All image sets have higher balanced accuracies and are more accurately segmented by trainable segmentation. It is also important to note that global thresholding still requires user input to refine the parameters of the threshold and select an appropriate thresholding algorithm to use. 

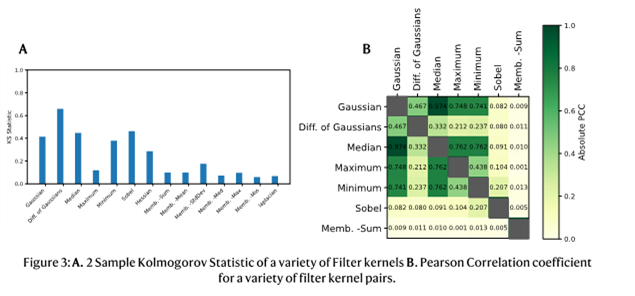
We have implemented a default selection of filter kernels in ParticleSpy that perform well across all image types. The key factors of the filter kernels considered are their effectiveness and similarity compared to other selected filter kernels, as many highly effective, similar filter kernels do not improve segmentation. Effectiveness and similarity can be analysed using the 2-sample Kolmogorov-Smirnov Statistic and the Pearson Correlation Coefficient (PCC) respectively ^[4]. The 2-sample Kolmogorov-Smirnov Statistic is a measure of the separation of two distributions, an effective filter kernel is more capable of separating particle and background pixel distributions. The Pearson Correlation Coefficient is a normalised measure of the correlation of two data sets. A high PCC value suggests the two filter kernels have segmented the image in a similar manner. The absolute PCC has been used here, as a perfect negative correlation simply means inverted labelling of the pixels, which does not contribute additional information to the classifier. Figure 3 shows the KS Statistic and PCC on a set of AuGe TEM images.   The most effective filter kernels are the Gaussian, Difference of Gaussians, Median, Minimum and Sobel filter kernels. The most similar of these are the Gaussian and Median filter kernels, and the most distinctive being the Difference of Gaussians and the Sobel filter kernel. The effectiveness and similarity of the filter kernels vary between image sets and can be tuned in ParticleSpy to each image type before classification.

Compared to global thresholding methods, trainable segmentation in ParticleSpy produces more accurate segmentations for a comparable quantity of user input, and its segmentation parameters can be highly customised, from the default set of parameters to the classifier used. It also offers the benefit that no pre-processing of the images is necessary. Trainable segmentation is not as accurate as segmentation using convolutional neural networks, but it is much faster to train and requires orders of magnitude fewer labelled pixels. The accessibility of ParticleSpy within Python will hopefully encourage wider use of trainable segmentation on electron microscope data sets.

References

[1]         T. J. A. Slater, E. A. Lewis, S. J. Haigh, Recent Progress in Scanning Transmission Electron Microscope Imaging and Analysis: Application to Nanoparticles and 2D Nanomaterials, 2016.

[2]      N. Otsu, IEEE Trans Syst Man Cybern 1979, SMC-9, 62.

[3]      I. Arganda-Carreras, V. Kaynig, C. Rueden, K. W. Eliceiri, J. Schindelin, A. Cardona, H. Sebastian Seung, Bioinformatics 2017, 33, 2424.

[4]      M. J. Slakter, J. Am. Stat. Assoc. 1965, 60, 854.